Atmosphere
Overview
Atmospheric modeling is essential for aerospace engineering, satellite operations, meteorology, and environmental science. These tools provide computational methods to characterize the Earth’s atmosphere at different altitudes and conditions, addressing how temperature, pressure, density, and composition vary with altitude, latitude, time, and solar activity.
The atmosphere is a complex, dynamic system influenced by gravitational compression, solar radiation, geomagnetic activity, and seasonal variations. Accurate atmospheric models are critical for aircraft performance calculations, rocket trajectory analysis, satellite drag estimation, and atmospheric reentry simulations.
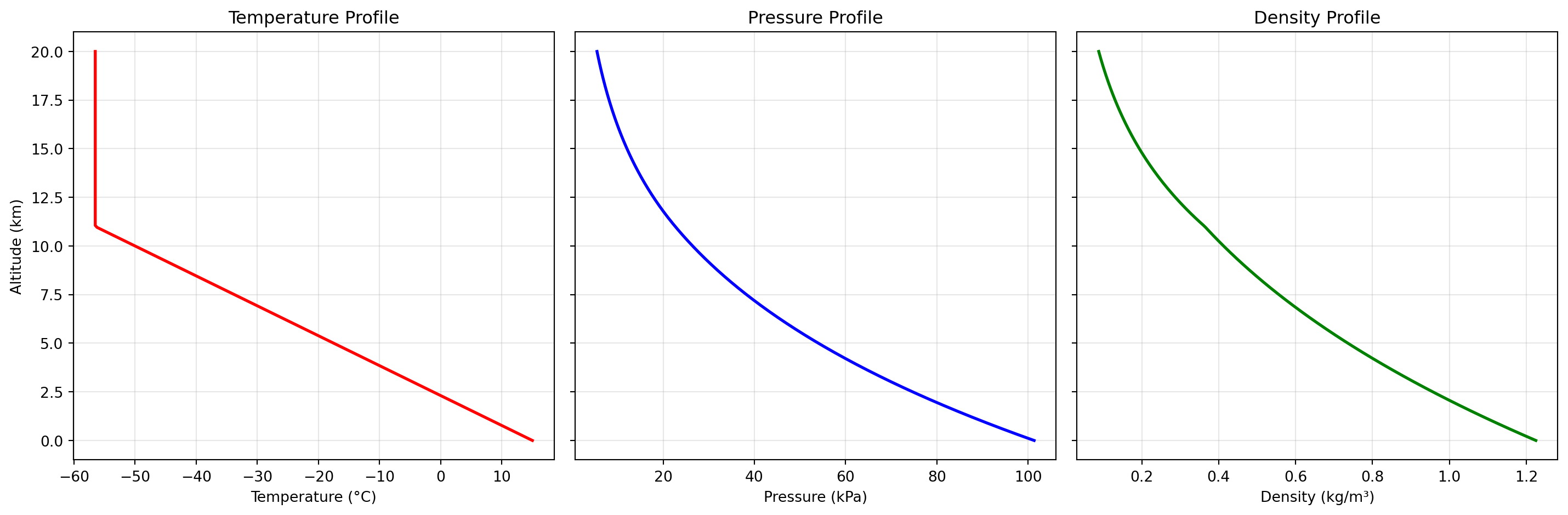
Standard Atmosphere Models like the US Standard Atmosphere 1976 provide baseline atmospheric properties as a function of altitude, assuming average mid-latitude conditions. The ATMOSPHERE_1976 tool implements this widely-used reference model, providing temperature, pressure, and density from sea level to 1000 km. These models divide the atmosphere into layers (troposphere, stratosphere, mesosphere, thermosphere) with distinct temperature gradients, as shown in Figure 1.
Empirical Atmospheric Models like NRLMSISE-00 account for real-world variability including geographic location, time of day, solar activity, and geomagnetic conditions. The ATMOS_NRLMSISE00 tool uses this sophisticated model, particularly important for satellite operations where atmospheric drag varies significantly with solar cycles and geomagnetic storms. These models are implemented using Python libraries like NumPy for numerical computations.
Atmospheric Path Calculations determine the total mass of air along a line of sight through the atmosphere, critical for optical astronomy, remote sensing, and solar radiation modeling. The AIRMASS tool computes this quantity for any viewing angle and altitude, enabling corrections for atmospheric extinction and refraction effects.

AIRMASS
This function computes atmospheric air mass, which is the integrated mass of air per unit surface area along a line of sight through the atmosphere. It is commonly used in atmospheric science, optics, and solar engineering to quantify how much atmosphere a path traverses at a given viewing angle.
The model integrates density with geometric and refractive corrections as a function of elevation:
m(\gamma)=\int_0^{H_{max}} \rho(H)\left\{1-\left[1+2(RI-1)\left(1-\frac{\rho(H)}{\rho_0}\right)\right]\left[\frac{\cos\gamma}{1+H/R}\right]^2\right\}^{-1/2} dH
The density profile is supplied as tabulated height-density points and linearly interpolated between points. The angle is measured above the horizon, where 90^\circ corresponds to a vertical path with minimum air mass.
Excel Usage
=AIRMASS(density_profile, angle, h_max, r_planet, ri)density_profile(list[list], required): 2D array with elevation (m) in the first column and density (kg/m³) in the second columnangle(float, required): Angle above the horizon in degrees (0-90)h_max(float, optional, default: 86400): Maximum height to integrate to (m)r_planet(float, optional, default: 6371229): Radius of the planet (m)ri(float, optional, default: 1.000276): Refractive index of the atmosphere
Returns (float): Mass of air per square meter (float), or error message string.
Example 1: Zenith air mass (straight up)
Inputs:
| density_profile | angle | |
|---|---|---|
| 0 | 1.225 | 90 |
| 1000 | 1.112 |
Excel formula:
=AIRMASS({0,1.225;1000,1.112}, 90)Expected output:
96133.3
Example 2: Air mass at 45 degree angle
Inputs:
| density_profile | angle | h_max | r_planet | |
|---|---|---|---|---|
| 0 | 1.225 | 45 | 86400 | 6371229 |
| 1000 | 1.112 |
Excel formula:
=AIRMASS({0,1.225;1000,1.112}, 45, 86400, 6371229)Expected output:
135059
Example 3: All arguments specified explicitly
Inputs:
| density_profile | angle | h_max | r_planet | ri | |
|---|---|---|---|---|---|
| 0 | 1.225 | 90 | 86400 | 6371229 | 1.000276 |
| 1000 | 1.112 |
Excel formula:
=AIRMASS({0,1.225;1000,1.112}, 90, 86400, 6371229, 1.000276)Expected output:
96133.3
Example 4: Custom planet radius
Inputs:
| density_profile | angle | h_max | r_planet | ri | |
|---|---|---|---|---|---|
| 0 | 1.225 | 90 | 86400 | 7000000 | 1.000276 |
| 1000 | 1.112 |
Excel formula:
=AIRMASS({0,1.225;1000,1.112}, 90, 86400, 7000000, 1.000276)Expected output:
96133.3
Python Code
Show Code
from fluids.atmosphere import airmass as fluids_airmass
def airmass(density_profile, angle, h_max=86400, r_planet=6371229, ri=1.000276):
"""
Calculate the mass of air per square meter in the atmosphere along a given angle using a density profile.
See: https://fluids.readthedocs.io/fluids.atmosphere.html
This example function is provided as-is without any representation of accuracy.
Args:
density_profile (list[list]): 2D array with elevation (m) in the first column and density (kg/m³) in the second column
angle (float): Angle above the horizon in degrees (0-90)
h_max (float, optional): Maximum height to integrate to (m) Default is 86400.
r_planet (float, optional): Radius of the planet (m) Default is 6371229.
ri (float, optional): Refractive index of the atmosphere Default is 1.000276.
Returns:
float: Mass of air per square meter (float), or error message string.
"""
# Helper to normalize 2D list input
def to2d(x):
return [[x]] if not isinstance(x, list) else x
try:
# Normalize density_profile input
density_profile = to2d(density_profile)
# Validate density_profile
if not isinstance(density_profile, list) or len(density_profile) < 2:
return "Error: density_profile must be a 2D list with at least two rows."
if not all(isinstance(row, list) and len(row) >= 2 for row in density_profile):
return "Error: density_profile must contain rows with at least two columns."
try:
heights = [float(row[0]) for row in density_profile]
densities = [float(row[1]) for row in density_profile]
except Exception:
return "Error: density_profile must contain numeric values."
if any(h2 <= h1 for h1, h2 in zip(heights, heights[1:])):
return "Error: heights in density_profile must be strictly increasing."
try:
gamma = float(angle)
h_max_val = float(h_max)
r_planet_val = float(r_planet)
ri_val = float(ri)
except Exception:
return "Error: angle, h_max, r_planet, and ri must be numbers."
if not (0 <= gamma <= 90):
return "Error: angle must be between 0 and 90 degrees."
if h_max_val <= 0:
return "Error: h_max must be positive."
if r_planet_val <= 0:
return "Error: r_planet must be positive."
if ri_val <= 0:
return "Error: ri must be positive."
# Linear interpolation function for density
def density_func(H):
if H <= heights[0]:
return densities[0]
if H >= heights[-1]:
return densities[-1]
for i in range(1, len(heights)):
if H < heights[i]:
h0, h1 = heights[i-1], heights[i]
d0, d1 = densities[i-1], densities[i]
return d0 + (d1 - d0) * (H - h0) / (h1 - h0)
return densities[-1]
result = fluids_airmass(density_func, gamma, h_max_val, r_planet_val, ri_val)
return result
except Exception as e:
return f"Error: {str(e)}"Online Calculator
ATMOS_NRLMSISE00
This function computes atmospheric temperature, mass density, and pressure using the NRLMSISE-00 empirical atmosphere model. The model supports conditions from near ground level to the upper atmosphere and accounts for geophysical inputs including location, day-of-year, and solar flux.
The pressure value reported by this model interface is derived from ideal-gas relationships applied to modeled species densities and temperature:
P = \rho R T
Inputs include altitude, latitude, longitude, time-of-year, and solar activity proxies (f107 and f107_{avg}). Results are returned as a single-row 2D array for spreadsheet compatibility.
Excel Usage
=ATMOS_NRLMSISE00(z, latitude, longitude, day, seconds, daily_flux, avg_flux)z(float, required): Elevation above sea level in meters.latitude(float, optional, default: 0): Latitude in degrees (-90 to 90).longitude(float, optional, default: 0): Longitude in degrees (-180 to 180).day(int, optional, default: 0): Day of year (0-366).seconds(float, optional, default: 0): Seconds since start of day (UT1 time).daily_flux(float, optional, default: 150): Daily average 10.7 cm solar flux.avg_flux(float, optional, default: 150): 81-day average solar flux.
Returns (list[list]): 2D list [[Temperature, Density, Pressure]], or error string.
Example 1: Standard Atmosphere at 1 km
Inputs:
| z | latitude | longitude | day | seconds | daily_flux | avg_flux |
|---|---|---|---|---|---|---|
| 1000 | 0 | 0 | 0 | 0 | 150 | 150 |
Excel formula:
=ATMOS_NRLMSISE00(1000, 0, 0, 0, 0, 150, 150)Expected output:
| Result | ||
|---|---|---|
| 293.656 | 1.05754 | 89219.1 |
Example 2: Mid-latitude Summer Day at 5 km
Inputs:
| z | latitude | longitude | day | seconds | daily_flux | avg_flux |
|---|---|---|---|---|---|---|
| 5000 | 45 | 45 | 180 | 0 | 150 | 150 |
Excel formula:
=ATMOS_NRLMSISE00(5000, 45, 45, 180, 0, 150, 150)Expected output:
| Result | ||
|---|---|---|
| 263.506 | 0.733251 | 55509.5 |
Example 3: High Altitude at Equator (20 km)
Inputs:
| z | latitude | longitude | day | seconds | daily_flux | avg_flux |
|---|---|---|---|---|---|---|
| 20000 | 0 | 0 | 100 | 0 | 150 | 150 |
Excel formula:
=ATMOS_NRLMSISE00(20000, 0, 0, 100, 0, 150, 150)Expected output:
| Result | ||
|---|---|---|
| 206.28 | 0.0955605 | 5663.17 |
Example 4: Custom Solar Flux at 10 km
Inputs:
| z | latitude | longitude | day | seconds | daily_flux | avg_flux |
|---|---|---|---|---|---|---|
| 10000 | 30 | -90 | 50 | 36000 | 200 | 180 |
Excel formula:
=ATMOS_NRLMSISE00(10000, 30, -90, 50, 36000, 200, 180)Expected output:
| Result | ||
|---|---|---|
| 227.886 | 0.424547 | 27795 |
Python Code
Show Code
from fluids.atmosphere import ATMOSPHERE_NRLMSISE00 as fluids_ATMOSPHERE_NRLMSISE00
def atmos_nrlmsise00(z, latitude=0, longitude=0, day=0, seconds=0, daily_flux=150, avg_flux=150):
"""
Compute temperature, density, and pressure using the NRLMSISE-00 atmospheric model.
See: https://fluids.readthedocs.io/fluids.atmosphere.html
This example function is provided as-is without any representation of accuracy.
Args:
z (float): Elevation above sea level in meters.
latitude (float, optional): Latitude in degrees (-90 to 90). Default is 0.
longitude (float, optional): Longitude in degrees (-180 to 180). Default is 0.
day (int, optional): Day of year (0-366). Default is 0.
seconds (float, optional): Seconds since start of day (UT1 time). Default is 0.
daily_flux (float, optional): Daily average 10.7 cm solar flux. Default is 150.
avg_flux (float, optional): 81-day average solar flux. Default is 150.
Returns:
list[list]: 2D list [[Temperature, Density, Pressure]], or error string.
"""
try:
# Validate input types and ranges
z = float(z)
latitude = float(latitude)
longitude = float(longitude)
day = int(day)
seconds = float(seconds)
daily_flux = float(daily_flux)
avg_flux = float(avg_flux)
except Exception:
return "Error: Invalid input types."
try:
if not (-90 <= latitude <= 90):
return "Error: latitude must be between -90 and 90 degrees."
if not ((-180 <= longitude <= 180) or (0 <= longitude <= 360)):
return "Error: longitude must be between -180 and 180 degrees or 0 and 360 degrees."
if not (0 <= day <= 366):
return "Error: day must be between 0 and 366."
result = fluids_ATMOSPHERE_NRLMSISE00(z, latitude, longitude, day, seconds, daily_flux, avg_flux)
T = float(result.T)
rho = float(result.rho)
P = float(result.P)
return [[T, rho, P]]
except Exception as e:
return f"Error: {str(e)}"Online Calculator
ATMOSPHERE_1976
This function evaluates atmospheric state and transport properties using the U.S. Standard Atmosphere 1976 model at a specified geometric altitude. It returns temperature, pressure, density, gravitational acceleration, dynamic viscosity, thermal conductivity, and speed of sound.
The model represents a piecewise-standard atmosphere with optional temperature offset dT applied to the standard profile. It is valid from below sea level up to the lower thermosphere range used by the 1976 standard.
For the returned pressure and density behavior, hydrostatic balance and gas-law relations are embedded in the atmospheric formulation:
\frac{dP}{dz}=-\rho g, \qquad P=\rho R T
The output is structured as a single-row 2D array for Excel compatibility.
Excel Usage
=ATMOSPHERE_1976(z, dt)z(float, required): Elevation above sea level in meters (valid range -610 to 86000 m).dt(float, optional, default: 0): Temperature offset from standard conditions in Kelvin.
Returns (list[list]): [[T, P, rho, g, mu, k, v_sonic]] where T is temperature (K), P is pressure (Pa), rho is density (kg/m^3), g is gravity (m/s^2), mu is dynamic viscosity (Pa·s), k is thermal conductivity (W/m/K), and v_sonic is speed of sound (m/s). str: Error message if input is invalid or out-of-range.
Example 1: Standard atmosphere at 5,000 m elevation
Inputs:
| z | dt |
|---|---|
| 5000 | 0 |
Excel formula:
=ATMOSPHERE_1976(5000, 0)Expected output:
| Result | ||||||
|---|---|---|---|---|---|---|
| 255.676 | 54048.3 | 0.736428 | 9.79124 | 0.0000162825 | 0.0227319 | 320.546 |
Example 2: Sea level standard atmosphere
Inputs:
| z | dt |
|---|---|
| 0 | 0 |
Excel formula:
=ATMOSPHERE_1976(0, 0)Expected output:
| Result | ||||||
|---|---|---|---|---|---|---|
| 288.15 | 101325 | 1.225 | 9.80665 | 0.0000178938 | 0.0253259 | 340.294 |
Example 3: Below sea level atmosphere (-500 m)
Inputs:
| z | dt |
|---|---|
| -500 | 0 |
Excel formula:
=ATMOSPHERE_1976(-500, 0)Expected output:
| Result | ||||||
|---|---|---|---|---|---|---|
| 291.4 | 107478 | 1.28489 | 9.80819 | 0.0000180502 | 0.025581 | 342.208 |
Example 4: Custom temperature offset at 10,000 m
Inputs:
| z | dt |
|---|---|
| 10000 | -5 |
Excel formula:
=ATMOSPHERE_1976(10000, -5)Expected output:
| Result | ||||||
|---|---|---|---|---|---|---|
| 218.252 | 26499.9 | 0.422984 | 9.77587 | 0.000014304 | 0.0196395 | 296.159 |
Python Code
Show Code
from fluids.atmosphere import ATMOSPHERE_1976 as fluids_atmosphere_1976
def atmosphere_1976(z, dt=0):
"""
Calculate standard atmospheric properties at a given altitude using the US Standard Atmosphere 1976 model.
See: https://fluids.readthedocs.io/fluids.atmosphere.html
This example function is provided as-is without any representation of accuracy.
Args:
z (float): Elevation above sea level in meters (valid range -610 to 86000 m).
dt (float, optional): Temperature offset from standard conditions in Kelvin. Default is 0.
Returns:
list[list]: [[T, P, rho, g, mu, k, v_sonic]] where T is temperature (K), P is pressure (Pa), rho is density (kg/m^3), g is gravity (m/s^2), mu is dynamic viscosity (Pa·s), k is thermal conductivity (W/m/K), and v_sonic is speed of sound (m/s). str: Error message if input is invalid or out-of-range.
"""
try:
z_val = float(z)
dt_val = float(dt)
if not (-610 <= z_val <= 86000):
return "Error: z must be between -610 and 86000 meters."
atm = fluids_atmosphere_1976(z_val, dT=dt_val)
result = [
atm.T,
atm.P,
atm.rho,
atm.g,
atm.mu,
atm.k,
atm.v_sonic
]
return [result]
except Exception as e:
return f"Error: {str(e)}"Online Calculator