One Sample Tests
Overview
One-sample tests are fundamental statistical procedures that compare a single sample of data against a known standard, theoretical value, or hypothesized probability distribution. Rather than comparing two or more groups, one-sample tests examine whether the characteristics of your data significantly differ from an established baseline or expectation. These tests form the foundation of hypothesis testing and are among the first analytical tools used in statistical inference.
What One-Sample Tests Answer
One-sample tests address critical questions such as: “Is the mean height of this group equal to the national average?” “Does this data follow a normal distribution?” or “Is the median income significantly different from $50,000?” By formalizing these questions as testable hypotheses, one-sample tests provide a rigorous framework for making statistical inferences about populations based on sample data.
Underlying Implementation
The one-sample testing framework is implemented through SciPy’s scipy.stats module, which provides robust, numerically optimized implementations of various one-sample tests. These implementations handle edge cases, compute test statistics efficiently, and return p-values and confidence intervals suitable for scientific and business decision-making.
Two Major Categories of One-Sample Tests
One-sample tests are organized into two distinct categories based on their purpose:
Location Tests (Testing the Mean or Median)
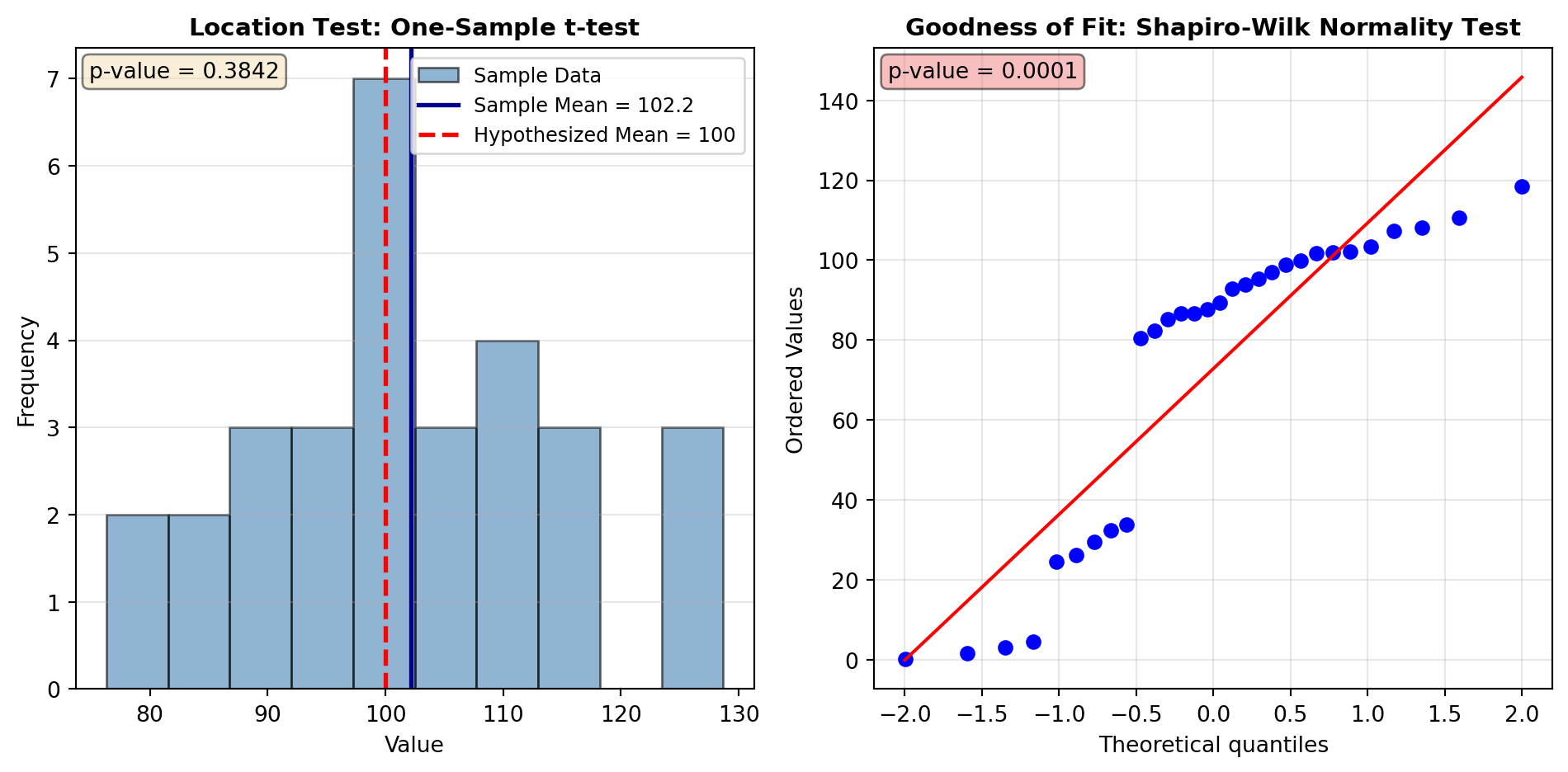
These tests determine whether the central tendency of your sample differs significantly from a hypothesized value. The one-sample t-test (TTEST_1SAMP) is the most widely used location test, examining whether a sample mean differs from a known value under the assumption of normality. It’s applicable when you have continuous data from a roughly normal distribution. The QUANTILE_TEST extends this concept to any quantile of the distribution, not just the mean, providing greater flexibility for skewed or non-normal data.
Goodness of Fit Tests (Testing Distribution Shape)
These tests evaluate whether your sample data follows a specific theoretical distribution, typically the normal distribution. Several complementary approaches exist: the SHAPIRO test is the most powerful for detecting departures from normality across a range of alternatives and is particularly effective for small to moderate sample sizes. The NORMALTEST (Anderson-Darling test) provides an omnibus normality test suitable for larger samples. The JARQUE_BERA test combines information about skewness and kurtosis, making it efficient for large samples. The KSTEST (Kolmogorov-Smirnov test) is a flexible, distribution-free test that works for any continuous distribution, not just the normal. For specialized distributional characteristics, the SKEWTEST and KURTOSISTEST specifically test whether skewness or kurtosis differ from normal distribution values.
Discrete and Binomial Data
When working with categorical or binary outcome data, the BINOMTEST tests whether the observed proportion of successes in a sequence of independent trials matches a hypothesized probability. This is essential for yes/no experiments, defect rates, conversion rates, and other binary outcomes.
When to Use Each Tool
Use location tests (TTEST_1SAMP, QUANTILE_TEST) when you want to test whether your sample’s central value differs from a known or hypothesized value. Use goodness of fit tests (SHAPIRO, NORMALTEST, JARQUE_BERA, KSTEST, SKEWTEST, KURTOSISTEST) to verify whether your data meets distributional assumptions before applying parametric tests or to validate that data conforms to expected behavior. Use the binomial test (BINOMTEST) for binary response variables or proportion data.
The visualization below illustrates the complementary roles of location tests and goodness of fit tests in hypothesis testing:

Tools
| Tool | Description |
|---|---|
| BINOMTEST | Perform a binomial test for the probability of success in a Bernoulli experiment. |
| JARQUE_BERA | Perform the Jarque-Bera goodness of fit test for normality. |
| KSTEST | Performs the one-sample Kolmogorov-Smirnov test for goodness of fit. |
| KURTOSISTEST | Test whether the kurtosis of a sample is different from that of a normal distribution. |
| NORMALTEST | Test whether a sample differs from a normal distribution (omnibus test). |
| QUANTILE_TEST | Perform a quantile test to determine if a population quantile equals a hypothesized value. |
| SHAPIRO | Perform the Shapiro-Wilk test for normality. |
| SKEWTEST | Test whether the skewness of a sample is different from that of a normal distribution. |
| TTEST_1SAMP | Perform a one-sample t-test for the mean of a group of scores. |