Multivariate Distributions
Overview
Multivariate distributions describe the joint probability behavior of two or more random variables simultaneously. Unlike univariate distributions that model a single random variable in isolation, multivariate distributions capture the correlations, dependencies, and joint behavior of multiple variables—an essential capability for understanding complex systems where variables interact. These distributions form the foundation for statistical modeling, machine learning, Bayesian inference, and risk analysis across finance, engineering, biology, and countless other domains.
Background and Importance: In practice, most real-world phenomena involve multiple correlated quantities. Financial portfolios contain multiple asset returns; manufacturing processes have correlated dimensions; ecological systems involve interdependent populations; medical diagnostics combine multiple biomarkers. Understanding how these variables relate requires multivariate probability models that capture their joint distribution rather than treating each variable independently. Multivariate distributions provide the mathematical framework for conditional probability, partial correlation analysis, and prediction under uncertainty in multivariate settings.
Implementation: These tools leverage SciPy statistical distributions, which implement efficient sampling, density computation, and parameter estimation for the most commonly used multivariate distributions. The implementations support both parametric analysis through probability density/mass functions and computational inference through random sampling.
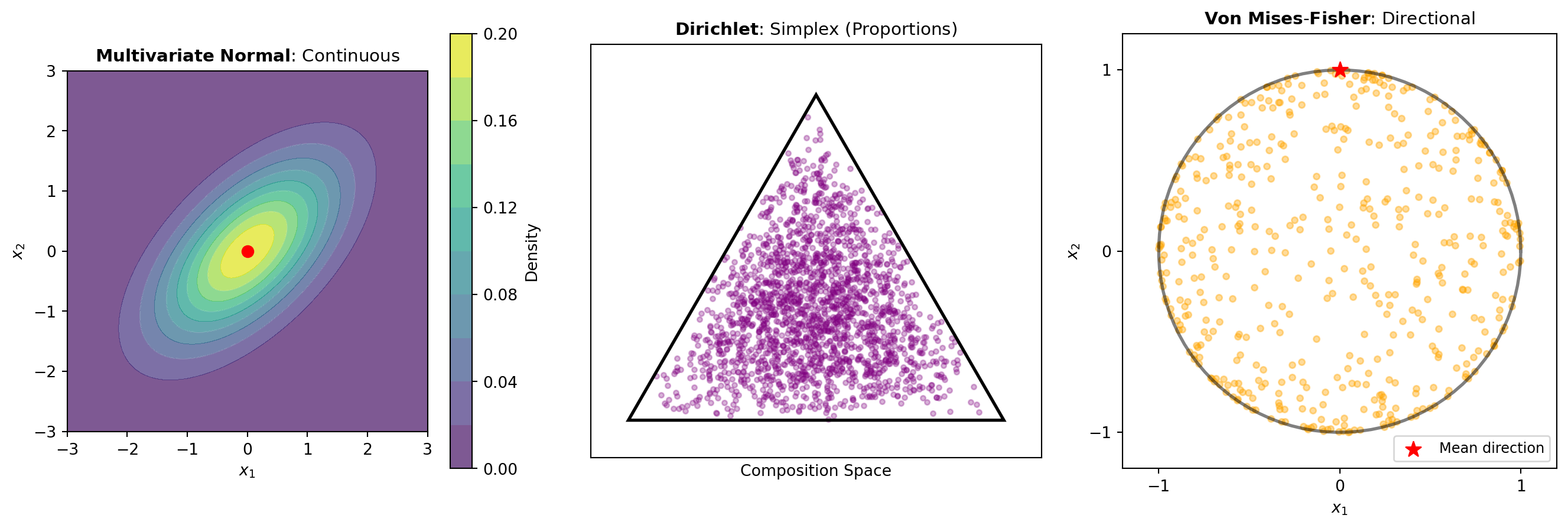
Normal Models: The MULTIVARIATE_NORMAL distribution is the workhorse of multivariate statistics, generalizing the univariate normal distribution to multiple dimensions. It is specified by a mean vector and covariance matrix, making it essential for linear regression, Gaussian process modeling, and Kalman filtering. The MULTIVARIATE_T distribution extends this to handle heavier tails, providing robustness against outliers in multivariate data. These normal-based models assume smooth, bell-shaped relationships between variables and are appropriate when data exhibits approximately linear dependencies and symmetric variations.
Simplex-Constrained Distributions: When variables represent proportions or probabilities that must sum to one, simplex-constrained models become essential. The DIRICHLET distribution is the fundamental model for compositional data—situations where observations represent relative frequencies or proportions. It is conjugate to the multinomial distribution, making it ideal for Bayesian models of categorical outcomes. The MULTINOMIAL distribution extends the binomial distribution to multiple categories, modeling counts across mutually exclusive classes. The DIRICHLET_MULTINOM combines these, providing a hierarchical model with overdispersion useful for count data with extra variability. Use these distributions when modeling topic distributions in text, allele frequencies in genetics, or budget allocations across categories.
Counting and Sampling Distributions: The MV_HYPERGEOM distribution extends hypergeometric sampling to multiple categories, modeling draws without replacement from a finite population with multiple types. This is essential for survey sampling and quality control problems where exhausting the population matters.
Matrix-Valued Distributions: When the random object itself is a matrix—not just a multivariate vector—specialized distributions apply. The MATRIX_NORMAL distribution models random matrices with structured covariance across rows and columns, useful in multivariate regression and spatial data analysis. The WISHART distribution models random positive-definite matrices, serving as the conjugate prior for covariance matrices in Bayesian analysis and appearing naturally in multivariate analysis of variance (MANOVA).
Directional and Rotational Distributions: Many applications involve directional data on spheres or rotation matrices. The VONMISES_FISHER distribution models directional data on the unit hypersphere—observations with a preferred direction and concentration around it. This applies to wind directions, protein orientations, and circular outcomes in geographic data. The UNIFORM_DIRECTION distribution generates uniformly distributed directions on the hypersphere, useful for simulating isotropic random orientations. For random orthogonal and unitary matrices, the ORTHO_GROUP, SPECIAL_ORTHO_GROUP, and UNITARY_GROUP distributions sample from Haar measures—the natural uniform distributions on rotation and unitary groups. Finally, RANDOM_CORRELATION generates random correlation matrices with specified spectral properties, useful for testing statistical methods and sensitivity analysis in multivariate settings.
Figure 1 illustrates key distinctions across these distribution families: the normal model capturing continuous multivariate relationships, the simplex-constrained Dirichlet handling compositional data, and the von Mises-Fisher directing observations on the sphere.

Tools
| Tool | Description |
|---|---|
| DIRICHLET | Computes the PDF, log-PDF, mean, variance, covariance, entropy, or draws random samples from a Dirichlet distribution. |
| DIRICHLET_MULTINOM | Computes the probability mass function, log probability mass function, mean, variance, or covariance of the Dirichlet multinomial distribution. |
| MATRIX_NORMAL | Computes the PDF, log-PDF, or draws random samples from a matrix normal distribution. |
| MULTINOMIAL | Compute the probability mass function, log-PMF, entropy, covariance, or draw random samples from a multinomial distribution. |
| MULTIVARIATE_NORMAL | Computes the PDF, CDF, log-PDF, log-CDF, entropy, or draws random samples from a multivariate normal distribution. |
| MULTIVARIATE_T | Computes the PDF, CDF, or draws random samples from a multivariate t-distribution. |
| MV_HYPERGEOM | Computes probability mass function, log-PMF, mean, variance, covariance, or draws random samples from a multivariate hypergeometric distribution. |
| ORTHO_GROUP | Draws random samples of orthogonal matrices from the O(N) Haar distribution using scipy.stats.ortho_group. |
| RANDOM_CORRELATION | Generates a random correlation matrix with specified eigenvalues. |
| SPECIAL_ORTHO_GROUP | Draws random samples from the special orthogonal group SO(N), returning orthogonal matrices with determinant +1. |
| UNIFORM_DIRECTION | Draws random unit vectors uniformly distributed on the surface of a hypersphere in the specified dimension. |
| UNITARY_GROUP | Generate a random unitary matrix of dimension N from the Haar distribution. |
| VONMISES_FISHER | Computes the PDF, log-PDF, entropy, or draws random samples from a von Mises-Fisher distribution on the unit hypersphere. |
| WISHART | Computes the PDF, log-PDF, or draws random samples from the Wishart distribution using scipy.stats.wishart. |