Differentiation
Overview
Differentiation is a fundamental operation in calculus that measures how a function changes as its input varies. The derivative of a function at a point represents the instantaneous rate of change or the slope of the tangent line at that point. This concept extends naturally to multivariable functions through partial derivatives, which measure how the function changes with respect to one variable while holding others constant.
In computational and applied mathematics, differentiation serves critical roles across diverse domains. In optimization, derivatives identify where functions reach minima or maxima. In sensitivity analysis, they quantify how model outputs respond to parameter changes. In physics and engineering, derivatives describe velocities, accelerations, gradients, and flux. In machine learning, derivatives drive gradient-based training algorithms for neural networks.
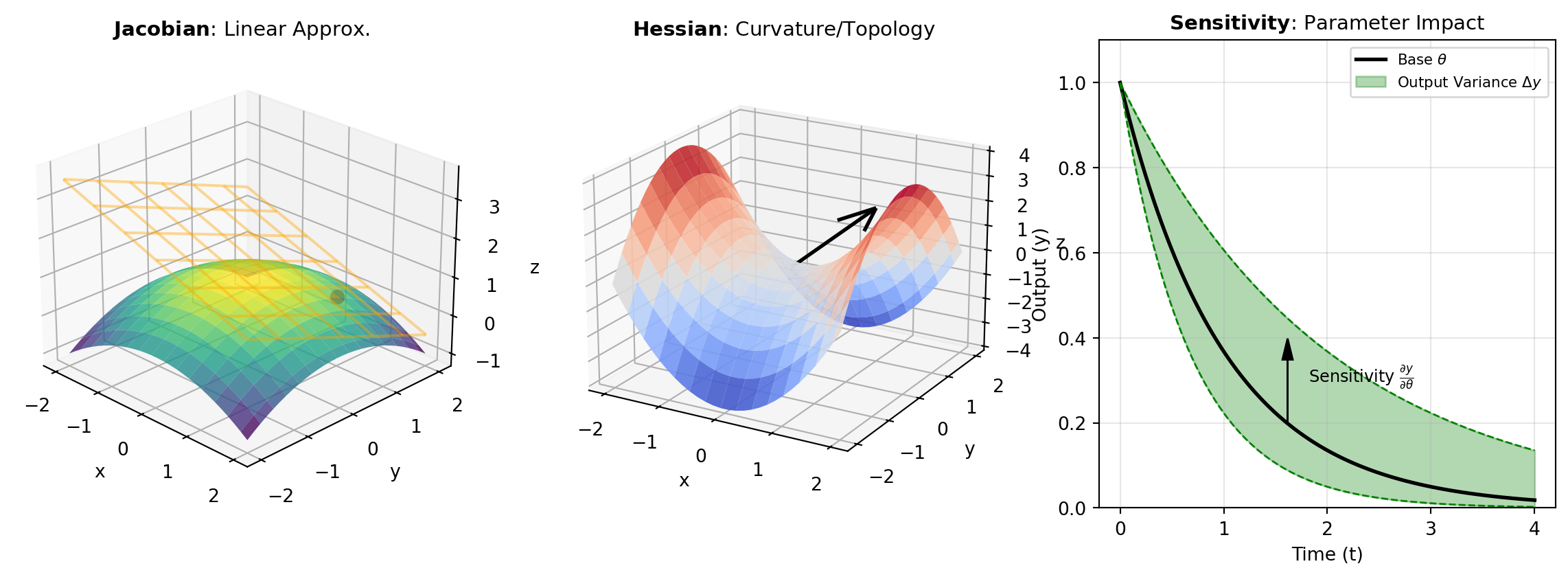
When working with multivariate functions, first and second derivatives organize into matrix structures that capture the complete landscape of function behavior. Figure 1 illustrates the hierarchy of derivative structures: the gradient captures first-order information for scalar functions, the Jacobian generalizes this to vector-valued functions, and the Hessian captures second-order curvature information essential for optimization.
Jacobian Matrix
The Jacobian matrix is the matrix of all first-order partial derivatives of a vector-valued function. For a function \mathbf{f}: \mathbb{R}^n \to \mathbb{R}^m that maps n inputs to m outputs, the Jacobian \mathbf{J} is an m \times n matrix where entry J_{ij} = \frac{\partial f_i}{\partial x_j}.
The Jacobian serves multiple purposes: - Linear approximation: Near a point, \mathbf{f}(\mathbf{x} + \Delta\mathbf{x}) \approx \mathbf{f}(\mathbf{x}) + \mathbf{J}\Delta\mathbf{x} - Coordinate transformations: The Jacobian determinant describes how volumes change under coordinate transformations - Optimization: Newton’s method for systems of equations requires the Jacobian to update iterates - Machine learning: Backpropagation uses Jacobians (chain rule) to compute gradients
The JACOBIAN function computes this matrix using symbolic differentiation, enabling automatic and exact derivative calculation for complex mathematical expressions.
Hessian Matrix
The Hessian matrix is the square matrix of second-order partial derivatives of a scalar-valued function. For f: \mathbb{R}^n \to \mathbb{R}, the Hessian \mathbf{H} is an n \times n symmetric matrix where H_{ij} = \frac{\partial^2 f}{\partial x_i \partial x_j}.
The Hessian characterizes the local curvature of a function and is essential for: - Optimization: Determines whether critical points are minima, maxima, or saddle points via the second derivative test - Newton-type methods: Newton’s method uses \mathbf{x}_{k+1} = \mathbf{x}_k - \mathbf{H}^{-1}\nabla f for quadratic convergence - Uncertainty quantification: The inverse Hessian approximates the covariance of parameter estimates in maximum likelihood estimation - Stability analysis: Eigenvalues of the Hessian indicate stability of dynamical systems at equilibria
The HESSIAN function computes this matrix symbolically using CasADi, a powerful framework for algorithmic differentiation.
Sensitivity Analysis
Sensitivity analysis quantifies how variations in model parameters affect model outputs. In the context of differentiation, local sensitivity is measured by the derivative \frac{\partial y}{\partial \theta}, where y is the model output and \theta is a parameter.
Sensitivity analysis is critical for: - Model validation: Identifying which parameters most influence predictions - Parameter estimation: Understanding parameter identifiability and correlation - Uncertainty propagation: Computing how input uncertainties affect outputs via error propagation: \sigma_y^2 \approx \sum_i \left(\frac{\partial y}{\partial \theta_i}\right)^2 \sigma_{\theta_i}^2 - Experimental design: Determining which parameters to measure more carefully - Robust design: Finding parameter settings that minimize output variance
The SENSITIVITY function automates this computation for scalar models, providing the gradient of outputs with respect to all model parameters.
Native Excel Capabilities
Excel provides limited built-in capabilities for numerical differentiation: - Manual finite differences: Users can implement finite difference formulas like f'(x) \approx \frac{f(x+h) - f(x)}{h} using cell formulas, but this requires manual setup and careful choice of step size h - Solver sensitivity reports: The Solver Add-in provides sensitivity information (shadow prices, reduced costs) for linear and nonlinear programming problems after optimization - Chart trendlines: Trendline equations can be differentiated analytically by hand, but Excel doesn’t compute derivatives automatically
These approaches have significant limitations: - No symbolic differentiation (only numerical approximation) - Numerical derivatives suffer from truncation and round-off errors - No automatic computation of Jacobians or Hessians - Manual implementation is error-prone and tedious for complex functions
The Python functions in this library use CasADi for symbolic differentiation, which provides exact derivatives without numerical approximation errors and efficiently handles complex multivariable functions.
Third-party Excel Add-ins
- Analytic Solver (Frontline Systems): Provides advanced optimization capabilities with enhanced sensitivity reporting, including marginal analysis and parametric sensitivity for nonlinear models.
- ASAP Utilities: While primarily a productivity tool, includes some numerical analysis helpers, though not specifically focused on differentiation.
- xlwings: A Python-Excel integration tool that allows users to call Python libraries (including CasADi, SymPy, or NumPy) from Excel, enabling custom differentiation workflows.
Tools
| Tool | Description |
|---|---|
| HESSIAN | Compute the Hessian matrix (second derivatives) of a scalar function using CasADi symbolic differentiation. |
| JACOBIAN | Calculate the Jacobian matrix of mathematical expressions with respect to specified variables. |
| SENSITIVITY | Compute the sensitivity of a scalar model with respect to its parameters using CasADi. |