Linear Algebra

Overview

Linear algebra is the mathematical study of vectors, matrices, and linear transformations. It provides the foundational framework for solving systems of linear equations, performing coordinate transformations, and analyzing multidimensional data. Modern applications span machine learning (where data and model parameters are represented as matrices), computer graphics (3D transformations and projections), signal processing (filtering and compression), quantum mechanics (state vectors and operators), and econometrics (multiple regression and cointegration analysis).

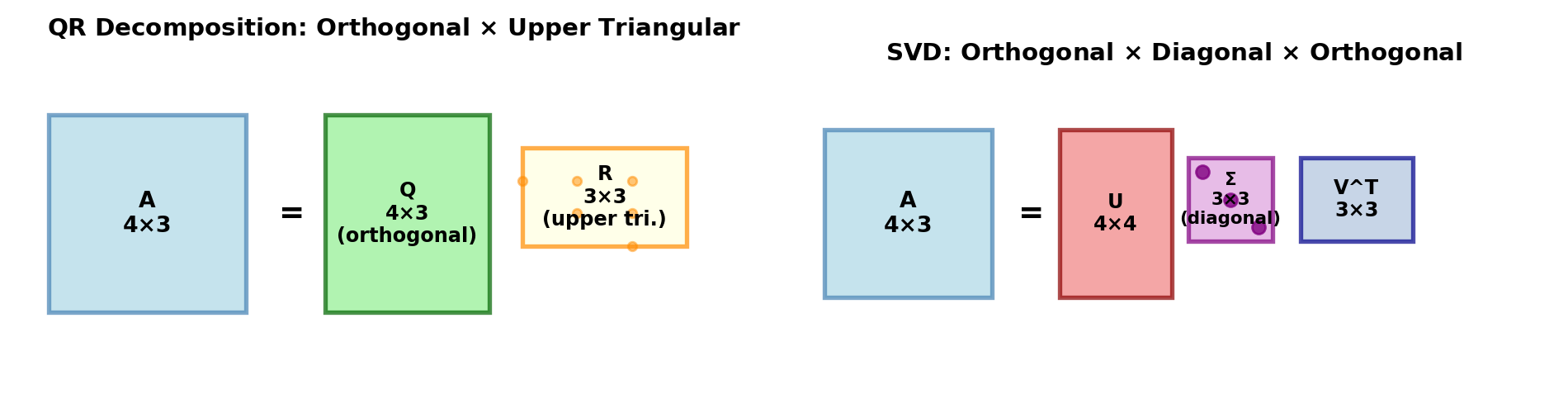
At the heart of linear algebra are several core decompositions that factorize a matrix into simpler components. These decompositions not only reveal the underlying structure of data but also enable efficient and numerically stable algorithms for solving complex problems.

Matrix Decompositions

Matrix decompositions break down a matrix into products of simpler matrices, revealing fundamental properties and enabling efficient computation.

Singular Value Decomposition (SVD) is perhaps the most powerful and general decomposition. It factorizes any m \times n matrix A as A = U \Sigma V^H, where U and V are orthogonal (or unitary) matrices and \Sigma is a diagonal matrix of singular values. SVD applications include: - Dimensionality reduction: Principal Component Analysis (PCA) uses SVD to find the directions of maximum variance - Low-rank approximation: Truncating small singular values produces optimal matrix approximations for data compression - Recommender systems: Collaborative filtering uses SVD to discover latent factors in user-item matrices - Signal denoising: Retaining only the largest singular values filters out noise

QR Decomposition factors a matrix A into an orthogonal matrix Q and an upper triangular matrix R such that A = QR. This decomposition is central to: - Solving linear systems: QR is numerically more stable than Gaussian elimination for ill-conditioned matrices - Gram-Schmidt orthogonalization: Constructing orthonormal bases from arbitrary vectors - Eigenvalue algorithms: The QR algorithm is the most common method for computing eigenvalues

Cholesky Decomposition is a specialized factorization for symmetric positive-definite matrices, expressing A = LL^T where L is lower triangular. Because it requires half the operations of LU decomposition, Cholesky is the preferred method for: - Covariance matrices: Efficient storage and inversion in multivariate statistics - Monte Carlo simulation: Generating correlated random variables - Numerical optimization: Many Newton-type methods use Cholesky to solve the Hessian system

Least-Squares Problems

Least-squares is the problem of finding the vector x that minimizes \|Ax - b\|_2. When A has more rows than columns (an overdetermined system), no exact solution typically exists, so we seek the x that makes the residual as small as possible.

Unconstrained least-squares is solved by the normal equations A^T A x = A^T b, but this approach can be numerically unstable. Modern implementations use QR or SVD for greater accuracy. The LSTSQ function provides a robust general-purpose solver for linear regression, curve fitting, and system identification.

Bounded least-squares extends the framework by adding box constraints l \leq x \leq u on the solution. The LSQ_LINEAR function solves these problems using trust-region methods, critical for applications where physically meaningful solutions require non-negative coefficients (e.g., chemical concentrations) or lie within known bounds (e.g., portfolio weights).

Pseudoinverse

The Moore-Penrose pseudoinverse A^+ generalizes the concept of matrix inversion to rectangular and singular matrices. When A is invertible, A^+ = A^{-1}; otherwise, A^+ provides the “best” generalized inverse in a least-squares sense. Computed via SVD, the PINV function is used for: - Solving least-squares problems: x = A^+ b gives the minimum-norm least-squares solution - Finding minimal solutions: When multiple solutions exist, the pseudoinverse yields the one with the smallest norm - Control theory: Computing the controllability and observability Gramians

Matrix Functions

Beyond decompositions, certain matrix functions extend familiar scalar operations to matrices. The matrix exponential e^A is defined by the power series e^A = I + A + \frac{A^2}{2!} + \frac{A^3}{3!} + \cdots and plays a central role in: - Differential equations: The solution to \frac{d\mathbf{x}}{dt} = A\mathbf{x} is \mathbf{x}(t) = e^{At}\mathbf{x}(0) - Markov chains: Continuous-time transition probabilities are computed via e^{Qt} - Lie group theory: The exponential map connects Lie algebras to Lie groups, used in robotics and computer vision

The EXPM function efficiently computes the matrix exponential using scaling and squaring with Padé approximation, as implemented in scipy.linalg.expm.

Native Excel capabilities

Excel provides basic linear algebra operations but lacks the specialized decompositions and advanced solvers needed for modern applications: - MMULT: Matrix multiplication - TRANSPOSE: Matrix transposition - MINVERSE: Matrix inversion (limited to square invertible matrices) - MDETERM: Determinant calculation - LINEST: Multiple linear regression via ordinary least squares

These functions handle small problems adequately but offer no access to: - SVD, QR, or Cholesky decompositions - Pseudoinverse computation - Bounded or constrained least-squares - Matrix exponential or other matrix functions - Numerical stability controls (e.g., singular value thresholds, choice of LAPACK driver)

Python functions provide full access to the battle-tested SciPy Linear Algebra module, enabling robust, high-performance computations on large matrices.

Third-party Excel add-ins

XLSTAT: Offers PCA (via SVD) and advanced regression tools, though linear algebra decompositions are not directly exposed as matrix functions.
NumXL: Provides econometric and time-series tools with matrix operations, but focuses on statistical modeling rather than low-level linear algebra primitives.
MATLAB Excel Link (via Python or COM): Enables calling MATLAB from Excel for full linear algebra capabilities, though this requires a MATLAB license and external integration.

For users needing production-grade linear algebra in Excel without external dependencies, Python in Excel with SciPy is the most comprehensive and accessible solution.

Tools

Tool	Description
CHOLESKY	Compute the Cholesky decomposition of a real, symmetric positive-definite matrix.
EXPM	Compute the matrix exponential of a square matrix using scipy.linalg.expm
LSQ_LINEAR	Solve a bounded linear least-squares problem.
LSTSQ	Compute the least-squares solution to Ax = B using scipy.linalg.lstsq.
PINV	Compute the Moore-Penrose pseudoinverse of a matrix using singular value decomposition (SVD).
QR	Compute the QR decomposition of a matrix and return either Q or R.
SVD	Compute the Singular Value Decomposition (SVD) of a matrix using scipy.linalg.svd.