ODE Models
Overview
Ordinary differential equations (ODEs) describe how a quantity changes over time as a function of its current state. They form the mathematical foundation for modeling dynamic systems across science and engineering. While the general-purpose ODE solvers handle arbitrary user-defined systems, many scientific disciplines rely on a core set of canonical models—well-studied systems with known behaviors, parameter interpretations, and real-world applications. These classic ODE models appear repeatedly across biology, chemistry, physics, and engineering, serving as both pedagogical tools and practical simulation frameworks.
Why Canonical Models? Rather than always deriving and solving custom differential equations, scientists and engineers repeatedly encounter the same fundamental systems. The Lotka-Volterra model describes predator-prey interactions in ecology. The SIR and SEIR models SEIR capture disease spread through populations. The Hodgkin-Huxley model explains neuronal action potentials in neuroscience. The Lorenz system demonstrates chaos and sensitive dependence on initial conditions. Each of these models has been extensively studied, validated against real data, and developed with well-understood parameters that have scientific meaning. Pre-built implementations eliminate the need to translate research papers into code and allow you to focus on application, calibration, and interpretation.
Implementation: These tools leverage SciPy’s scipy.integrate.solve_ivp function for numerical integration, supplemented by specialized solvers where appropriate. SciPy provides flexible, production-ready ODE integration routines with support for stiff systems, event detection, and dense output. The implementations handle parameterization, initial conditions, and time spans, making these classic systems immediately usable in analysis pipelines and simulations.
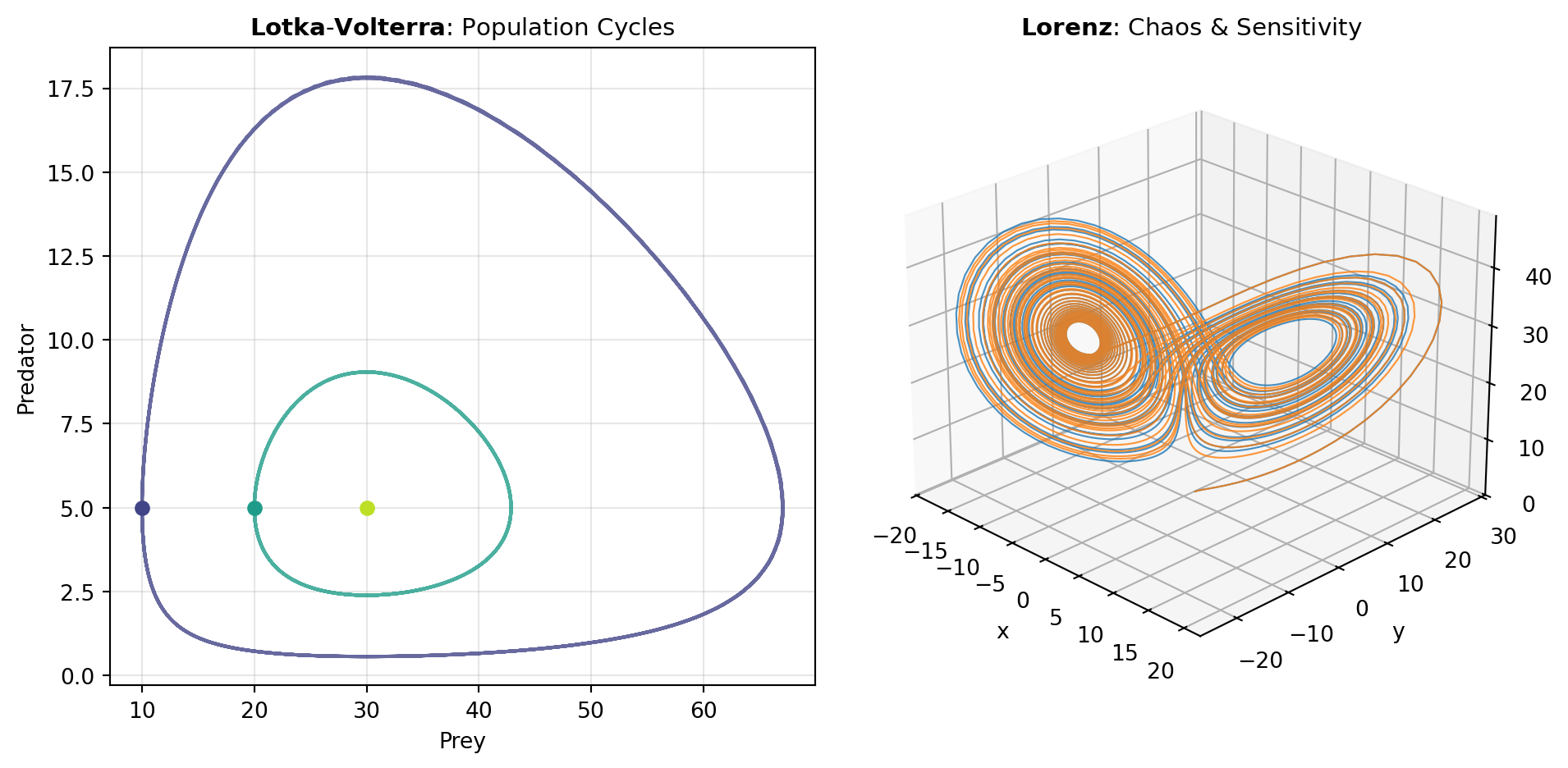
Biological and Ecological Models: Population dynamics follow predictable patterns when modeled with differential equations. The Lotka-Volterra model captures the cyclic oscillations between predator and prey populations—as prey increase, predators thrive; as predators consume prey, their food supply dwindles, leading to population crashes. Epidemiological models like SIR and SEIR partition populations into compartments (Susceptible, Infected, Recovered, and for SEIR, Exposed) and track flow between compartments, enabling prediction of epidemic peaks, herd immunity thresholds, and intervention effectiveness. The COMPARTMENTAL_PK model extends this compartmental thinking to pharmacokinetics, describing how drug concentrations change through absorption, distribution, and elimination. The MICHAELIS_MENTEN model characterizes enzyme kinetics, revealing how reaction rate saturates with substrate concentration—a critical principle in biochemistry.
Neuronal and Physical Systems: The nervous system relies on rapid electrical signaling, modeled through ODEs capturing ion channel dynamics. The Hodgkin-Huxley model provides the canonical biophysical description of action potentials, with separate equations for sodium, potassium, and leak currents. For situations requiring simpler neuronal abstractions, the FitzHugh-Nagumo model reduces the Hodgkin-Huxley complexity to two variables while retaining essential dynamics like excitability and refractoriness. The Van der Pol oscillator exemplifies nonlinear oscillations with limit cycles—self-sustained oscillations that appear across biology, electronics, and mechanical systems.
Chemical and Chaotic Systems: Chemical reaction networks often yield oscillatory behavior despite the second law of thermodynamics. The Brusselator is a paradigmatic autocatalytic reaction mechanism demonstrating how coupling autocatalytic and cross-catalytic steps produces sustained oscillations. Beyond these biochemical systems, the Lorenz system stands as the archetypal example of deterministic chaos: three coupled ODEs with parameters chosen to produce trajectories that never settle into equilibrium yet depend sensitively on initial conditions—a system that fundamentally altered understanding of dynamics and predictability.
Figure 1 illustrates characteristic behaviors of several canonical ODE models, showing how diverse phenomena—from population cycling to neuronal firing to chaotic orbits—emerge from different system architectures.
When to Use Each Tool: Start with SIR or SEIR for disease dynamics and public health modeling. Use LOTKA_VOLTERRA for basic ecological predator-prey scenarios. For neuroscience, choose HODGKIN_HUXLEY when biophysical accuracy is essential or FITZHUGH_NAGUMO for speed and conceptual clarity. Pharmaceutical applications require COMPARTMENTAL_PK or MICHAELIS_MENTEN. Chemical oscillations appear in BRUSSELATOR, and chaos studies use LORENZ. The VAN_DER_POL oscillator serves as a standard nonlinear oscillator benchmark across many disciplines.

Tools
| Tool | Description |
|---|---|
| BRUSSELATOR | Numerically solves the Brusselator system of ordinary differential equations for autocatalytic chemical reactions. |
| COMPARTMENTAL_PK | Numerically solves the basic one-compartment pharmacokinetics ODE using scipy.integrate.solve_ivp. |
| FITZHUGH_NAGUMO | Numerically solves the FitzHugh-Nagumo system of ordinary differential equations for neuron action potentials using scipy.integrate.solve_ivp. |
| HODGKIN_HUXLEY | Numerically solves the Hodgkin-Huxley system of ordinary differential equations for neuron action potentials. |
| LORENZ | Numerically solves the Lorenz system of ordinary differential equations for chaotic dynamics. |
| LOTKA_VOLTERRA | Numerically solves the Lotka-Volterra predator-prey system of ordinary differential equations. |
| MICHAELIS_MENTEN | Numerically solves the Michaelis-Menten system of ordinary differential equations for enzyme kinetics using scipy.integrate.solve_ivp. |
| SEIR | Numerically solves the SEIR system of ordinary differential equations for infectious disease modeling using scipy.integrate.solve_ivp. |
| SIR | Solves the SIR system of ordinary differential equations for infection dynamics using scipy.integrate.solve_ivp (see scipy.integrate.solve_ivp). |
| VAN_DER_POL | Numerically solves the Van der Pol oscillator system of ordinary differential equations. |